Oscilador armónico forzado y amortiguado
Dos partículas, una de masa 100.000 veces más pesada que la otra, con fuerza elástica entre ellas. La partícula masiva permanece por tanto fija y la ligera oscila alrededor de la primera. Existe fricción que genera una fuerza de frenado -f*V. Y también se define una fuerza externa oscilatoria F=Fo*sin(w*t). Se trata del problema, resuelto teóricamente, del oscilador armónico forzado y amortiguado (driven damped oscillator). La fricción elimina rápidamente la oscilación a la frecuencia natural del oscilador w0, quedando una oscilación a la misma frecuencia que la fuerza externa, y con una amplitud que sigue la conocida curva dependiente de w/w0 y de la fricción.
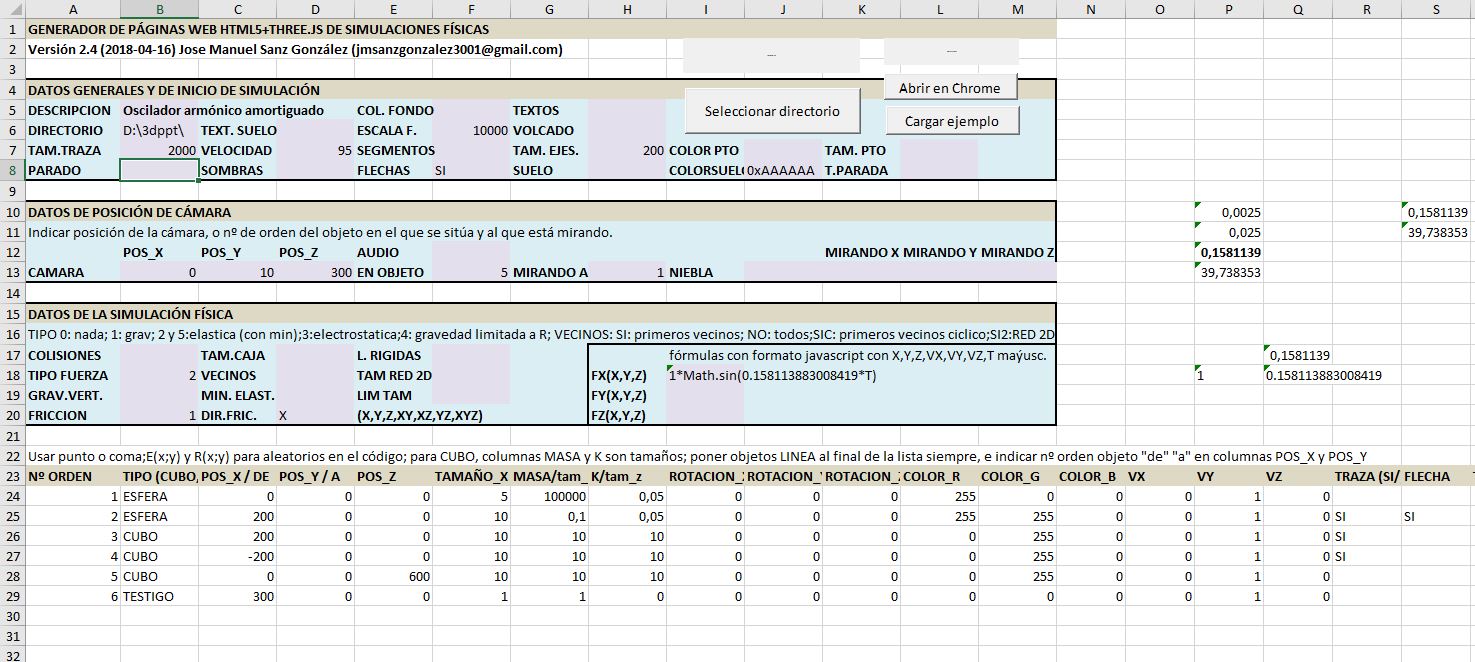
Esta simulación incorpora tres controles más, que permiten variar la Fo (amplitud de la fuerza externa), w/w0 y el factor f de fricción (la fuerza de fricción es F=-f*V). Los parámetros fijos de la simulación son la masa de la partícula m=0.1 y la constante de la fuerza elástica k=0.0025 (lo que da w0=0.158113883).
La simulación se inicia pulsando P o con el control para. El vector central corresponde a la fuerza externa oscilante (se representa en el centro, pero es la misma en todo el espacio).
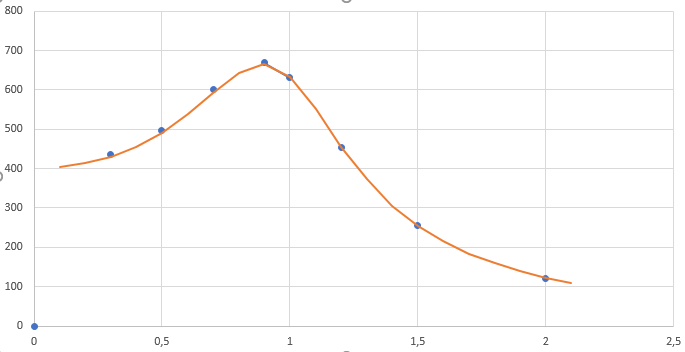
A modo de ejemplo, se reperesenta la gráfica obtenida para la amplitud de la oscilación vs w/w0 con f=0.1, Fo=1. Los puntos son los resultados de la simulación y la curva continua es la curva teórica.
Simular